La Trigonometría es la rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos. Los babilonios y los egipcios (hace mas de 3000 años) fueron los primeros en utilizar los ángulos de un triángulo y las razones trigonométricas para efectuar medidas en agricultura y para la construcción de pirámides. También se desarrollo a partir de los primeros esfuerzos hechos para avanzar en el estudio de la astronomía mediante la predicción de las rutas y posiciones de los cuerpos celestes y para mejorar la exactitud en la navegación y en el calculo del tiempo y los calendarios.
El estudio de la trigonometría pasó después a Grecia, en donde se destaca el matemático y astrónomo Griego Hiparco, por haber sido uno de los principales desarrolladores de la Trigonometría. Las tablas de “cuerdas” que construyo fueron las precursoras de las tablas de las funciones trigonométricas de la actualidad.
Desde Grecia, la trigonometría pasó a la India y Arabia donde era utilizada en la Astronomía. Y desde Arabia se difundió por Europa, donde finalmente se separa de la Astronomía para convertirse en una rama independiente que hace parte de la matemática.
Definiciones:
- El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.
- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

- Problemas con solución:
- 1.
- Corre, el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio a una altura de 1,5 m:
- Para comenzar, vamos a hacer un dibujo
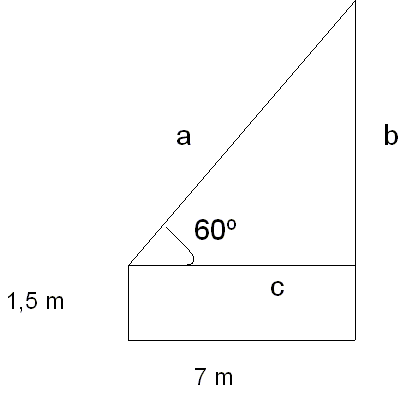 que aclare un poco la situación poniendo los datos que conocemos.Si nos fijamos en el triángulo, el lado c mide 7 m y una vez que tengamos calculado el lado b, para calcular la altura de la torre sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.Para el ángulo 60º, el lado que conozco es el cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo la tangente de 60º.
que aclare un poco la situación poniendo los datos que conocemos.Si nos fijamos en el triángulo, el lado c mide 7 m y una vez que tengamos calculado el lado b, para calcular la altura de la torre sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.Para el ángulo 60º, el lado que conozco es el cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo la tangente de 60º.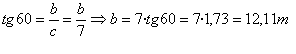 Por tanto la altura de la torre es 12,11 m + 1,5 m = 13, 61 m.
Por tanto la altura de la torre es 12,11 m + 1,5 m = 13, 61 m. - 2.
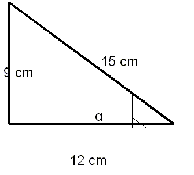 Como ves, los tres lados del triángulo son conocidos, así que para calcular las razones trigonométricas sólo tenemos que aplicar las fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y la hipotenusa 15.
Como ves, los tres lados del triángulo son conocidos, así que para calcular las razones trigonométricas sólo tenemos que aplicar las fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y la hipotenusa 15.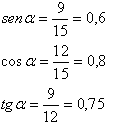
- Biografía Hipocrates:
- Médico griego. Según la tradición, Hipócrates descendía de una estirpe de magos de la isla de Cos y estaba directamente emparentado con Esculapio, el dios griego de la medicina. Contemporáneo de Sócrates y Platón, éste lo cita en diversas ocasiones en sus obras. Al parecer, durante su juventud Hipócrates visitó Egipto, donde se familiarizó con los trabajos médicos que la tradición atribuye a Imhotep.Aunque sin base cierta, se considera a Hipócrates autor de una especie de enciclopedia médica de la Antigüedad constituida por varias decenas de libros (entre 60 y 70). En sus textos, que en general se aceptan como pertenecientes a su escuela, se defiende la concepción de la enfermedad como la consecuencia de un desequilibrio entre los llamados humores líquidos del cuerpo, es decir, la sangre, la flema y la bilis amarilla o cólera y la bilis negra o melancolía, teoría que desarrollaría más tarde Galeno y que dominaría la medicina hasta la Ilustración.
 Para luchar contra estas afecciones, el corpus hipocrático recurre al cauterio o bisturí, propone el empleo de plantas medicinales y recomienda aire puro y una alimentación sana y equilibrada. Entre las aportaciones de la medicina hipocrática destacan la consideración del cuerpo como un todo, el énfasis puesto en la realización de observaciones minuciosas de los síntomas y la toma en consideración del historial clínico de los enfermos.En el campo de la ética de la profesión médica se le atribuye el célebre juramento que lleva su nombre, que se convertirá más adelante en una declaración deontológica tradicional en la práctica médica, que obliga a quien lo pronuncia, entre otras cosas, a «entrar en las casas con el único fin de cuidar y curar a los enfermos», «evitar toda sospecha de haber abusado de la confianza de los pacientes, en especial de las mujeres» y «mantener el secreto de lo que crea que debe mantenerse reservado».
Para luchar contra estas afecciones, el corpus hipocrático recurre al cauterio o bisturí, propone el empleo de plantas medicinales y recomienda aire puro y una alimentación sana y equilibrada. Entre las aportaciones de la medicina hipocrática destacan la consideración del cuerpo como un todo, el énfasis puesto en la realización de observaciones minuciosas de los síntomas y la toma en consideración del historial clínico de los enfermos.En el campo de la ética de la profesión médica se le atribuye el célebre juramento que lleva su nombre, que se convertirá más adelante en una declaración deontológica tradicional en la práctica médica, que obliga a quien lo pronuncia, entre otras cosas, a «entrar en las casas con el único fin de cuidar y curar a los enfermos», «evitar toda sospecha de haber abusado de la confianza de los pacientes, en especial de las mujeres» y «mantener el secreto de lo que crea que debe mantenerse reservado». - Aunque inicialmente atribuida en su totalidad a Hipócrates, la llamada colección hipocrática es en realidad un conjunto de escritos de temática médica que exponen tendencias diversas, que en ciertos casos pueden incluso oponerse entre sí. Estos escritos datan, por regla general, del período comprendido entre los años 450 y 350 a.C., y constituyen la principal fuente a través de la cual es posible hoy hacerse una idea de las prácticas y concepciones médicas anteriores a la época alejandrina.En esta colección, la llamada «Antigua medicina» es uno de los tratados más antiguos y más célebres y en él sugiere el autor, entre otras propuestas, investigar el origen del arte que practica, origen que halla en el deseo de ofrecer al ser humano un régimen de vida y, en especial, una forma de alimentación que se adapte de una manera completamente racional a la satisfacción de sus necesidades más inmediatas. Por este motivo, considera por ejemplo el aprendizaje de la correcta cocción de los alimentos como una primera manifestación de la búsqueda de una existencia mejor.Por otro lado, los textos de la colección hipocrática demuestran sin lugar a dudas que la práctica de la observación precisa no era en el conjunto de la medicina griega una conquista de la época clásica, sino que más bien constituía una tradición sólidamente afianzada en el pasado y que a mediados del siglo V había alcanzado ya un notable nivel de desarrollo.

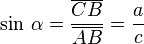
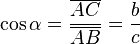
No hay comentarios:
Publicar un comentario